单个与成对捕食者的捕食策略和单个被捕食者的的逃跑策略
内容摘要
本文首先对单个被捕食者(双足食草恐龙)的几种逃跑策略和相应的捕食者(疾走食肉恐龙)的捕食策略进行分析和建模,被捕食者的捕食策略有与捕食者追捕方向直逃,根据捕食者的追捕进行预测先直线逃跑再转弯策略,对应的捕食者捕食策略有直追和先直线再转弯追捕。
对于单个疾走食肉恐龙的捕捉双足食草恐龙,建立的模型有双足食草恐龙径直逃跑和疾走食肉恐龙的追捕策略,双足食草恐龙以一定斜角逃跑及疾走食肉恐龙的追捕策略,双足食草恐龙先径直逃跑后待离疾走食肉恐龙不足一定距离时采取转弯策略,而转弯策略有转大角度固定向一边转弯,最大角度轮换向两边转弯,以最大转角最大地逃离疾走食肉恐龙距离的那边或距离到与疾走食肉恐龙追捕方向相反方向转弯,以随机角度转弯。经过几种模型的分析建模和比较,在单对单的捕食行为中,发现对疾走食肉恐龙来说采用直追,即被捕食者在哪就向哪跑去或向双足食草恐龙逃跑方向向前偏一点捕捉到双足食草恐龙的概率比较大,对双足食草恐龙来说则先采用径直地逃,待离疾走食肉恐龙为一定距离时再采取它的最大转弯角优势转弯,这种策略可提高生存概率,经模拟仿真,转弯时离疾走食肉恐龙的距离大约为1.7米。
在成对疾走食肉恐龙捕捉双足食草恐龙中,发现疾走食肉恐龙采用两边同时相向地向着双足食草恐龙包围跑去捕捉到的概率最大,而这种情况下双足食草恐龙先沿两疾走食肉恐龙连线的垂直平分线的方向的任一边直跑,待离任一疾走食肉恐龙的距离大约不足三米时再采取转弯策略最佳。
【关键词】:径直逃跑、转弯时相距距离、最大转弯角、先直线后转弯、matlab、建模、仿真、策略、径直追捕、预测、生存概率
一、问题的重述:
有一种疾走食肉恐龙(Velociraptor mongoliensis)生活在距今约7500万年前的白垩纪晚期。古生物学家认为它是顽强的捕猎者,可能成群地、并且一对一对地进行捕猎。可惜不可能像观察现代的食肉哺乳动物那样观察疾走食肉恐龙在野外的捕猎行为。古生物学家请你们队帮助对疾走食肉恐龙的捕猎行为进行建模。古生物学家希望将你们的结果与研究狮子、老虎以及类似的食肉动物的生物学家所报告的野外调查数据进行比较。
成年的疾走食肉恐龙一般身长3米,髋高0.5米,重约45公斤,据估计奔跑非常快,以每小时60公里的速度可持续奔跑约15秒钟,但是在以这样的速度冲刺之后,它需要停下来,通过在肌肉里增加乳酸使得体力恢复。
假定疾走食肉恐龙捕食与自己体型几乎相同的一种双足食草恐龙(Thescelosaurus neglectus)。对化石的生命力学分析揭示双足食草恐龙能以每小时50公里的速度长时间奔跑。
第一问:假设疾走食肉恐龙是孤单的捕猎者,建立数学模型,描述一只疾走食肉恐龙潜随和追猎一只双足食草恐龙的捕猎策略,以及被捕食者的逃避策略。假设双足食草恐龙在相距15米之内一定能觉察到疾走食肉恐龙,依赖于环境和气候条件可以在更大的范围内(一直到50米)觉察到。另外,由于身体结构和力量的缘故,疾走食肉恐龙在全速奔跑时的转弯半径是有限的,据估计,该半径是髋高的三倍。而双足食草恐龙却极其灵活,转弯半径仅为0.5米。
第二问:更符合实际地假设疾走食肉恐龙成对地去捕猎,建立新的模型,描述两只疾走食肉恐龙潜随和追猎一只双足食草恐龙的捕猎策略,以及被捕食者的逃避策略。继续使用第一问给出的其他假设。
三、符号的设定与假设
符号的设定:
d0:双足食草恐龙发现疾走食肉恐龙时的初始距离;
d:双足食草恐龙开始转弯时与疾走食肉恐龙的相距距离;
r1min:双足食草恐龙可能逃脱追捕的最小半径;
r2min:疾走食肉恐龙能抓住双足食草恐龙的最大半径;
t:捕食行为已经持续的时间(捕食行为开始时t=0);
dt:疾走食肉恐龙的反应时间,同时也为两恐龙的时间步长[1](反应时间是专门针对疾走食肉恐龙来说的,因为它要根据双足食草恐龙的奔跑而作出决断选择,需要反应时间), dt取值为0.05s~0.1s,两种恐龙的反应时间都是一样的,同时令时间步长也为dt,与反应时间一样为同一常量;
v1:双足食草恐龙的速度,v1=13.89m/s;
v2:疾走食肉恐龙的速度,v2=16.67m/s;
基于题意的假设:
1、仅当双足食草恐龙发现疾走食肉恐龙时,捕食行为才开始。
2、当疾走食肉恐龙追上双足食草恐龙或捕食行为持续了15秒,捕食行为结束。
3、由于疾走食肉恐龙全速奔跑只能持续15秒,因此超过15秒则认为捕食失败。
4、环境和气候条件的影响综合为双足食草恐龙发现疾走食肉恐龙的概率。
5、疾走食肉恐龙全速奔跑时最小转弯半径是1.5米,双足食草恐龙的为0.5米。
模型化的附加假设:
1一旦捕食行为开始,双方都不需要时间和位移,立即进入全速奔跑状态。[1]
2捕食行为发生在大平原上,没有山坡树林湖泊河流等障碍物的影响,恐龙可以以任意它们可以走的路线全速奔跑。
3两恐龙的奔跑可以分为一份一份进行的(相当于一跳一跳进行的),在时间步长内恐龙是直线前进的,在下一时间步长开始时恐龙才可以改变方向;
4反应时间是专门针对疾走食肉恐龙的,疾走食肉恐龙作出对双足食草恐龙的奔跑变化的反应需要时间;
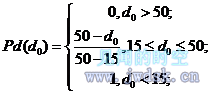
5双足食草恐龙发现疾走食肉恐龙的概率分布Pd是两者之间距离d0的函数:[1]
由函数可知离得越近发现的概率越大。
6根据一般的捕食模型(老虎、狮子等),捕食者总是径直地朝被捕食者扑去的,因此在模型构建中疾走食肉恐龙大多数时是径直地朝双足食草恐龙走去的。
四、模型构建及分析
一、基于单个疾走食肉恐龙的捕食策略与双足食草恐龙的逃跑策略
1、双足食草恐龙以与疾走食肉恐龙的追捕方向的方向逃跑(DE(directly escape)策略):
双足食草恐龙为了最慢地减少与疾走食肉恐龙的距离,可能会以这种策略逃跑。在这种情况下,先分析疾走食肉恐龙的捕食策略:一般来说,捕食者都是朝与被捕食者最快地减少距离的方向追捕的,因此疾走食肉恐龙采取的策略是径直地朝双足食草恐龙奔跑过去(DC(directly chase)策略),而双足食草恐龙也因此而径直地逃跑,结果是两者一前一后地径直追赶,设双足食草恐龙没被疾走食肉恐龙吃掉的最小距离为d0,则S0=(v2-v1) ×15s=41.67m,由附加假设6可知双足食草恐龙由于及早发现疾走食肉恐龙而没被吃掉的概率为
上面的概率是比较小的,因此双足食草恐龙要改变策略才求得更大生存概率。
2、双足食草恐龙以与疾走食肉恐龙的追捕方向成一定夹角的方向逃跑(OE(obliquity excape)策略):
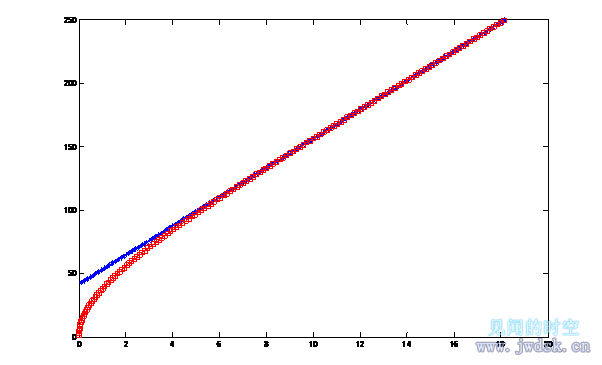
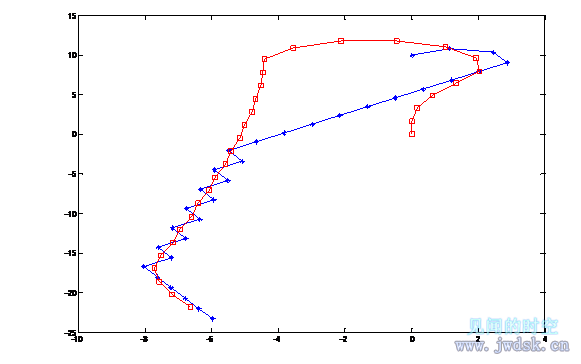
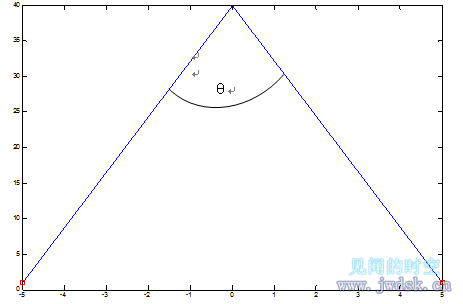
双足食草恐龙猜测疾走食肉恐龙会径直地追捕,因此会以一定斜角的方向逃跑,假设此时疾走食肉恐龙仍采用DC策略,设此角与疾走食肉恐龙的追捕方向的夹角为θ(角度制):如下图所示(下图假设θ=5度,用matlab作图,在matlab命令窗口中输入OC(5,42) (程序见附录),-*-直线为双足食草恐龙的逃跑路线,-□-曲线为疾走食肉恐龙的追捕路线)。
(注意,图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
运行runOC.m(程序见附录),经过matlab仿真,θ从0度以1度为间隔度数变化到15度,令最初两恐龙的距离为41.7米,由结果可知,当θ大于3度时双足食草恐龙将被疾走食肉恐龙捕捉到。可见,以一定角度逃跑不如上一DE策略的逃跑更佳。
3、双足食草恐龙先直线逃跑后以最小半径转弯逃跑(DFTL(directly first turn around later)策略)
基于上两策略,最开始时以DE策略逃跑是最佳的,因为这样使得与疾走食肉恐龙的相对速度最小,最大程度地避免捕食,但当最初距离小于41.67米时以这种策略双足食草恐龙最终是要被捕捉到的,因此双足食草恐龙会利用它的全速最小转弯半径为0.5米,比疾走食肉恐龙的全速最小转弯半径1.5米小得多的优势来提高救生概率,所以双足食草恐龙径直逃跑到与疾走食肉恐龙相距一定距离d时会转弯,与疾走食肉恐龙周旋以拖延时间,此时捕食行为已经进行了t了。在此模型中,当两恐龙相距小于或等于d时双足食草恐龙就会转弯。
这里假设有三种情况:
(1)、双足食草恐龙只会向一个方向转弯(如下图所示):
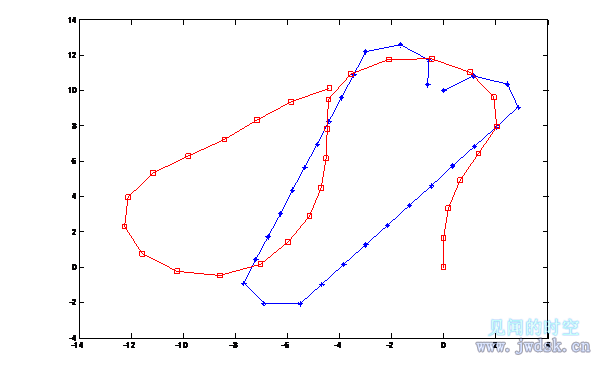
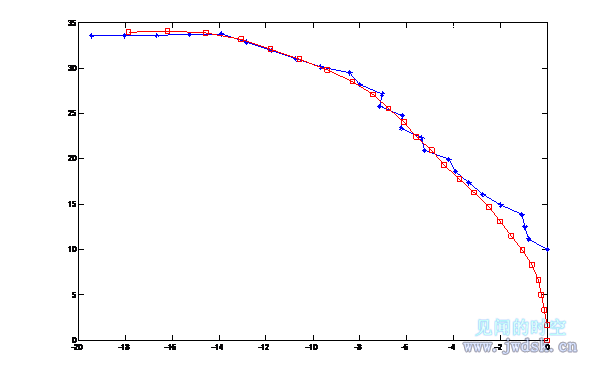
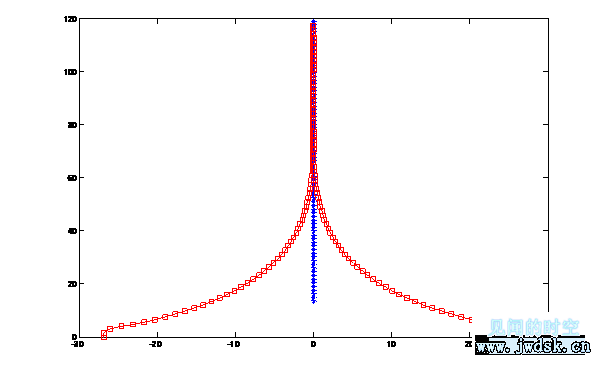
这种策略中,当双足食草恐龙发现被直追且两恐龙相距小于一定距离时,双足食草恐龙将以最大地更改方向,且只向一边转弯。见下图:
(说明:-□-为疾走食肉恐龙的追捕足迹,-*-为双足食草恐龙的逃跑足迹,(0,0)点是疾走食肉恐龙的起点,图形只画出双足食草恐龙改变方向后的足迹,前面的直线忽略,上图是当t=9s,d=35-(v2-v1)×9=10m时的情况,此情况下双足食草恐龙被捉到了。)
(注意,图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
用matlab进行仿真,程序见附录;程序是以最初距离d0从15米到50米变化,t从0秒到14秒变化,先设步长为1,运行程序runDFTL1.m(程序见附录);由程序仿真可得:
t
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
没被捕获的最小的do(m)
50
50
50
50
50
50
50
50
50
50
50
50
50
42
41
对应的d(m)
50
47.2
44.4
41.7
38.9
36.1
33.3
30.6
27.8
25
22.2
19.4
16.7
5.9
2.1
由上表可看出当转弯时t小于或等于13秒时,没被捕获的最小d0大于或等于42米,比径直逃跑还要糟糕,因此转弯时间应大于13秒。下面用程序从13秒变化到14.8秒,最初相距距离d0从39米变化到41.6米,步长为0.1;运行程序runDFTL11.m(程序见附录);得到下面数据:
|
t |
13 |
13.1 |
13.2 |
13.3 |
13.4 |
13.5 |
13.6 |
13.7 |
13.8 |
13.9 |
14 |
14.1 |
|
没被捕获的最小的do(m) |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
39.5 |
39.8 |
40.1 |
40.3 |
40.6 |
40.9 |
|
对应的d(m) |
5.49 |
5.21 |
4.93 |
4.66 |
4.38 |
4.1 |
1.72 |
1.74 |
1.77 |
1.69 |
1.71 |
1.73 |
|
t |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
14.7 |
14.8 |
|
||||
|
没被捕获的最小的do(m) |
41.2 |
41.4 |
41.4 |
41.6 |
41.6 |
41.6 |
41.6 |
|
||||
|
对应的d(m) |
1.76 |
1.68 |
1.4 |
1.32 |
1.04 |
0.77 |
0.49 |
|
||||
由上表可知,当相距d大约为1.7米时再转弯最好,这种情况下转弯甚至可以使最初相距d0为39.5米也没被捉到,从而提高生存概率,在一次捕食行为中这种策略的最高的生存概率为
可见这种策略比一味直逃提高了不少生存希望。
(2)、双足食草恐龙有轮换地向两边方向转弯:
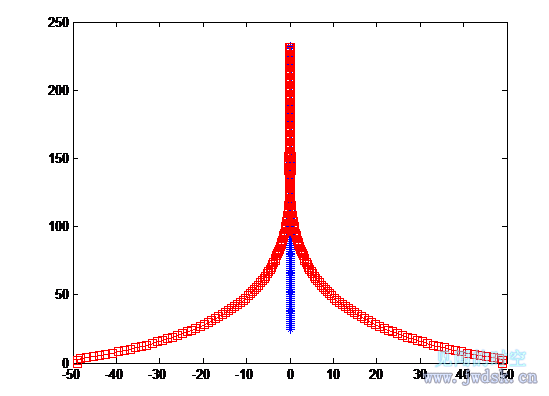
在上一转弯策略中,双足食草恐龙只会向一边转弯,实际情况不可能这样的,不断转弯有可能使自己固定在某个区域,因此双足食草恐龙会间隔地变换方向来逃生。如下图所示:
(说明:--□--为疾走食肉恐龙的追捕足迹,----为双足食草恐龙的逃跑足迹,(0,0)点是疾走食肉恐龙的起点,图形只画出双足食草恐龙改变方向后的足迹,前面的直线忽略,上图是当t=9s,d=35-(v2-v1)×9=10m时的情况,此情况下双足食草恐龙被捉到了。)
(注意,图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
用matlab进行仿真,程序见附录;程序是以最初距离d0从15米到50米变化,t从0秒到14秒变化,先设步长为1,运行程序runDFTL2.m(程序见附录);由程序仿真可得:
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
没被捕获的最小的do(m) |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
49 |
48 |
46 |
44 |
43 |
|
对应的d(m) |
50 |
47.2 |
44.4 |
41.7 |
38.9 |
36.1 |
33.3 |
30.6 |
27.8 |
25 |
21.2 |
17.4 |
12.7 |
7.9 |
4.1 |
由上面数据可知,当最初相距大于43米时,采取此种策略还不如直逃要好,因此取d0从40米变化到42米,t从14秒变化到14.8秒,步长为1,看看此种情况能否找到比直逃要好的方式,运行程序runDFTL22.m(程序见附录);由程序仿真可得如下数据:
|
t |
14 |
14.1 |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
14.7 |
14.8 |
|
没被捕获的最小的do(m) |
42 |
42 |
42 |
41.4 |
41.4 |
41.7 |
42 |
42 |
42 |
|
对应的d(m) |
3.11 |
2.83 |
2.56 |
1.68 |
1.4 |
1.42 |
1.44 |
1.17 |
0.89 |
由上面数据可知,相距距离d约为1.54米时转弯最好,这与上面的单向转弯策略得出的结论差不多,结合附加假设6,这种策略在一次捕食行为中的最高的获生概率为
由求得的概率可知比直跑的获生概率大了一点。
(3)、双足食草恐龙以逃离疾走食肉恐龙最远的方向逃跑
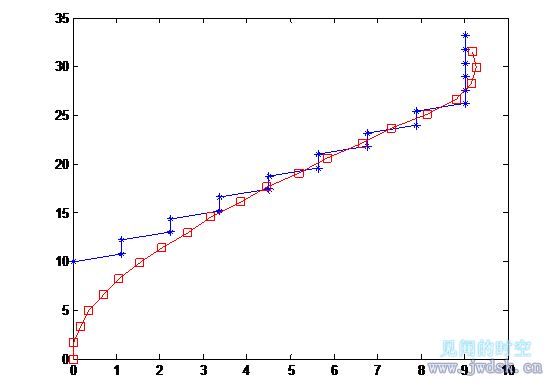
这种策略中,当双足食草恐龙发现被直追且两恐龙相距小于一定距离时,双足食草恐龙将最大地更改方向,方向取决于哪种方式离疾走食肉恐龙较远,或者使得双足食草恐龙的速度方向背离于疾走食肉恐龙的速度方向,见下图:
(说明:-□-为疾走食肉恐龙的追捕足迹,-*-为双足食草恐龙的逃跑足迹,(0,0)点是疾走食肉恐龙的起点,图形只画出双足食草恐龙改变方向后的足迹,前面的直线忽略,上图是当t=9s,d=35-(v2-v1)×9=10m时的情况,此情况下双足食草恐龙被捉到了。)
(注意,图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
用matlab进行仿真,程序见附录;程序是以最初距离d0从15米到50米变化,t从0秒到14秒变化,先设步长为1,运行程序runDFTL3.m(程序见附录);由程序仿真可得:
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
没被捕获的最小的do(m) |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
42 |
41 |
|
对应的d(m) |
50 |
47.2 |
44.4 |
41.7 |
38.9 |
36.1 |
33.3 |
30.6 |
27.8 |
25 |
22.2 |
19.4 |
16.7 |
5.89 |
2.1 |
由数据可知当t小于或等于12秒时,情况不如直逃好,因此取d0从38米变化到41.6米,t从13秒变化到14.8秒,步长为0.1,看看此种情况能否找到比直逃要好的方式,运行程序runDFTL33.m(程序见附录);由程序仿真可得如下数据:
|
t |
13 |
13.1 |
13.2 |
13.3 |
13.4 |
13.5 |
13.6 |
13.7 |
13.8 |
13.9 |
14 |
14.1 |
|
没被捕获的最小的do(m) |
41.6 |
41.6 |
41.6 |
41.6 |
38.9 |
39.2 |
39.5 |
39.8 |
40.1 |
40.3 |
40.6 |
40.9 |
|
对应的d(m) |
5.49 |
5.21 |
4.93 |
4.66 |
1.68 |
1.7 |
1.72 |
1.74 |
1.77 |
1.69 |
1.71 |
1.73 |
|
t |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
14.7 |
14.8 |
|
||||
|
没被捕获的最小的do(m) |
41.2 |
41.4 |
41.4 |
41.6 |
41.6 |
41.6 |
41.6 |
|
||||
|
对应的d(m) |
1.76 |
1.68 |
1.4 |
1.32 |
1.04 |
0.77 |
0.49 |
|
||||
对比上数据与DFTL1策略得到的数据可看出它们是差不多的,由于可见这种策略与DFTL1近似,由数据可知最小的d0为38.9,比DFTL1好一点,最佳的d大约为1.7,与上面得到的结论差不多。这种策略逃生概率大概为
4、双足食草恐龙先径直逃跑,后以一定的随机夹角最大地逃离疾走食肉恐龙(DFRL(directly first random run later)策略)
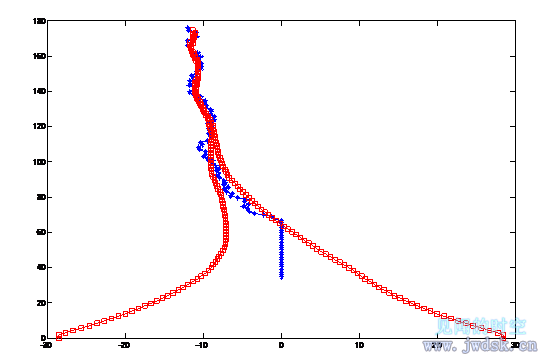
实际中双足食草恐龙不可能每次都以最大的转弯夹角转弯的,因此更接近现实是每次双足食草恐龙发现被直追且距离疾走食肉恐龙小于一定距离时会转弯,转弯的夹角是允许的随机角,随机角的正负取舍取决于哪个角更能远离疾走食肉恐龙。见下图:
(说明:-□-为疾走食肉恐龙的追捕足迹,-*-为双足食草恐龙的逃跑足迹,(0,0)点是疾走食肉恐龙的起点,图形只画出双足食草恐龙改变方向后的足迹,前面的直线忽略,上图是当t=9s,d=35-(v2-v1)×9=10m时的情况,此情况下双足食草恐龙被捉到了。)
(注意,由于是随机数是matlab随机产生的,因此每次运行程序得到的图形都很可能是不同的!图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
用matlab进行仿真,程序见附录;程序是以最初距离d0从15米到50米变化,t从0秒到14秒变化,先设步长为1,运行程序runDFTL4.m(程序见附录);在一次程序仿真中得到如下数据(每次运行此程序得到的数据都会有所不同,因为随机数是随机产生的):
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
没被捕获的最小的do(m) |
50 |
50 |
50 |
50 |
50 |
50 |
49 |
48 |
48 |
47 |
46 |
44 |
44 |
43 |
42 |
|
对应的d(m) |
50 |
47.2 |
44.4 |
41.7 |
38.9 |
36.1 |
32.33 |
28.56 |
25.78 |
22 |
18.22 |
13.44 |
10.37 |
6.89 |
3.11 |
由上表可看出当转弯时t小于13时,没被捕获的最小d0大于42米,比径直逃跑还要糟糕,因此转弯时间应大于13秒。下面用程序从13秒变化到14.8秒,最初相距距离d0从40米变化到41.6米,步长为0.1;运行程序runDFTL44.m(程序见附录);得到下面数据(每次运行此程序得到的数据都会有所不同,因为随机数是随机产生的):
|
t |
13 |
13.1 |
13.2 |
13.3 |
13.4 |
13.5 |
13.6 |
13.7 |
13.8 |
13.9 |
14 |
14.1 |
|
没被捕获的最小的do(m) |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.6 |
41.5 |
|
对应的d(m) |
5.49 |
5.21 |
4.93 |
4.66 |
4.38 |
4.1 |
3.82 |
3.54 |
3.27 |
2.99 |
2.71 |
2.33 |
|
t |
14.2 |
14.3 |
14.4 |
14.5 |
14.6 |
14.7 |
14.8 |
|
||||
|
没被捕获的最小的do(m) |
41.5 |
41.4 |
41.4 |
41.6 |
41.6 |
41.6 |
41.6 |
|
||||
|
对应的d(m) |
2.06 |
1.68 |
1.4 |
1.32 |
1.04 |
0.77 |
0.49 |
|
||||
由上表可看出,只有当转弯时两者相距d为2.06米、1.68米、1.4米时情况要比径直逃跑DE策略好,其余都不如径直逃跑,取三者平均值1.71米,这与DFTL2得到的1.54米是差不多的,即此种策略中当双足食草恐龙离疾走食肉恐龙为1.71米时采取随机转弯可获得比径直逃跑要大的逃生概率,此概率为
可知此概率与上面的DFTL2策略得到的大致是相同的。
由以上几种模型可知当双足食草恐龙离疾走食肉恐龙大约为1.7米时就要采取转弯策略,比较好的转弯策略为DFTL1。
二、基于成对疾走食肉恐龙的捕食策略与双足食草恐龙的逃跑策略
1、两边并排围捕策略
在这种策略中,两个疾走食肉恐龙是在两边悄悄地靠近双足食草恐龙的,设捕食开始时三恐龙为一等腰三角形,如下图所示:
(说明:□为疾走食肉恐龙的位置,顶角为为双足食草恐龙的位置,顶角大小设为θ。)
由于此情形下双足食草恐龙沿垂直于两疾走食肉恐龙连线方向逃跑是最快地远离危险的,因此设双足食草恐龙径直地远离逃跑,而两疾走食肉恐龙则向双足食草恐龙跑去。
设双足食草恐龙离疾走食肉恐龙的距离为d0;顶角为θ;如下图所示:
(说明:-□-为疾走食肉恐龙的追捕足迹,-*-为双足食草恐龙的逃跑足迹,(0,0)点是疾走食肉恐龙的起点,图形只画出双足食草恐龙改变方向后的足迹,前面的直线忽略,上图是当θ=45度,d0=30米时的情况,此情况下双足食草恐龙被捉到了。图中纵向和横向的两点间距有差异是因为纵坐标和横坐标的单位间距的长度不同造成的)
在matlab命令中输入two(55,45)再按enter键(two函数见附录),可以发现采取这种逃跑策略时,当d0=55米(大于最大发现疾走食肉恐龙距离),θ=45度时,双足食草恐龙最终还是被捕获,因此当发现两头双足食草恐龙从两边并排围过来时,双足食草恐龙采取这种策略很危险。
因此双足食草恐龙会采取转弯策略,如下图所示:
假设当双足食草恐龙离两疾走食肉恐龙的最近距离小于d时,双足食草恐龙会采取在允许的范围内随机转弯运动,θ取几个特殊值:180度,150度,120度,90度和60度,d0从42米变化到49米,d从1米变化到40米,在一次运行runtwoturn.m(程序见附录,此程序运算时间较长,大概要10分钟)中,捕获失败的数据如下:(由于双足食草恐龙改变方向的随机性,每次运行得到的数据都可能不同):
|
角度 |
60 |
90、 |
120、 |
150、 |
180、 |
|
d0取值 |
49(29点) |
49(5点) |
49、(11点) |
49、(24点) |
49(0点) |
|
捕获失败的d |
36、37、30、29、1~25 |
34、14、12、10、4 |
30、28、25、21、18、16、15、13、11、2、1 |
36、33、27、24、22、1~19 |
|
|
d0取值 |
48(26点) |
48(5点) |
48(4点) |
48(25点) |
48(1点) |
|
捕获失败的d |
31、29、1~24、 |
35、29、8、7、4、 |
23、18、10、4、 |
37、31、27~25、1~20 |
6 |
|
d0取值 |
47(20点) |
47(5点) |
47(6点) |
47(22点) |
47(0点) |
|
捕获失败的d |
29、23、21、1~17、 |
33、20、11、5、3、 |
32、17、16、10、8、7 |
31~33、26、24、23、1917、1~14 |
3 |
|
d0取值 |
46(16点) |
46(4点) |
46(7点) |
46(14点) |
46(0点) |
|
捕获失败的d |
29、1~15、 |
25、21、11、7、 |
22、17、8、6、5、3、2、 |
39、32、15、1~11 |
|
|
d0取值 |
45(12点) |
45(3) |
45(2点) |
45(10点) |
45(0点) |
|
捕获失败的d |
15、14、1~10、 |
26、22、7、 |
5、3、 |
32、1~9 |
|
|
d0取值 |
44、(15点) |
44、(1点) |
44、(2点) |
44、(12点) |
44(0点) |
|
捕获失败的d |
33、32、21、18、17、13、9~11、1~6 |
6、 |
16、4、 |
35、26、25、23、19、6~12 |
|
|
d0取值 |
43(10点) |
43(0点) |
43(1点) |
43(5点) |
43(1点) |
|
捕获失败的d |
35、31、27、20、16、11、9、7、6、2 |
|
4、 |
25、19、16、11、4、 |
10 |
|
d0取值 |
42(4点) |
42(2点) |
42(2点) |
42(6点) |
42(1点) |
|
捕获失败的d |
30、21、14、2、 |
7、3 |
4、3 |
18、17、15、14、12、11、 |
14 |
由上面的数据可以看出对疾走食肉恐龙来说,采取θ为180度时捕获失败的次数最少,而对双足食草恐龙来说,由于成功逃脱的d一般为3左右,因此距离疾走食肉恐龙的最小距离为3米左右时采取转弯最好。
2、包抄围捕
在这种策略中,两个疾走食肉恐龙中一个在一边静静地埋伏,另一个悄悄地绕到双足食草恐龙的另一边,然后绕到另一边的恐龙发起进攻,由上面单对单的捕食可知,此时双足食草恐龙一般会先采取径直逃跑策略,待双足食草恐龙走得离另一边埋伏的疾走食肉恐龙足够近时,埋伏多时的疾走食肉恐龙再发起进攻,此时由于埋伏的疾走食肉恐龙离双足食草恐龙比较近,由第一问分析可知如果双足食草恐龙在两者相距d0小于39.5米后才发现埋伏的疾走食肉恐龙,那太晚了,由于缺乏数据,在这种情况下什么时候双足食草恐龙发现埋伏的疾走食肉恐龙是很难确定的,因此难以用程序进行仿真,但可以确定的是这种围捕方式是非常佳的,因为奔跑中的双足食草恐龙由于担心身后的疾走食肉恐龙而分心,难以一时发现正在前方埋伏的恐龙,如果按照单对单的模型,双足食草恐龙很可能采取DFTL策略,这种策略是等到双足食草恐龙离疾走食肉恐龙大概1.7米时双足食草恐龙才转弯的,因此双足食草恐龙很可能跑进前面埋伏的疾走食肉恐龙的39.5米内的“死亡区域”,因此疾走食肉恐龙的捕获概率是很大的。
五、模型优缺点分析
模型的较为明显优点是对多种双足食草恐龙的逃跑策略进行模拟仿真,及分析相应的疾走食肉恐龙的对应策略,本论文的重点在对单对单追捕的分析,对成双对单的追捕分析较为粗糙。
最大缺点是没有利用到题目给的恐龙的身高身长体重的数据,这些在实际中影响也是很大的因素。还有假设中双足食草恐龙发现疾走食肉恐龙的概率分布实际中可能不是平均分布的。
附录
引用文献:
[1] 童中华、俞慧斌、李海明,追捕与逃跑策略,数学的实践与认识,第28卷第2期:179页至180页,1998年。
参阅文献:
1、尚玉昌,动物的捕食行为,生物学通报,第36卷第2期:14页,2001年。
2、孙鸾,猫科动物的捕食策略,生命世界,封面故事:24页到27页,2004年。


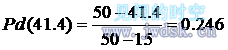

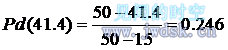


哎,看的这个就想起数学建模夏令营
@六娃:数学建模还是好怀念
@六娃 数学建模还是好怀念,怀念的其实是学生时代~
if((distance(d1,d2)((v2-v1)10))&&(k=(n-1)))
请问这个该怎么理解
@accjc:2010年华师的数学建模,那时拿了一等奖,但年代久远,matlab我都十几年没使用啦。。。
您好,请问有完整版代码吗?附件里的代码有很多缺失,我对题目理解也不是很透彻,楼主方便联系一下我吗?
希望楼主能看到QAQ,顶顶顶
同求完整代码
@yang:你们组团来的啊,代码要
代码在最下面的rar图标那里,点击下载的